Torsi atau puntiran merupakan fenomena mekanik yang sangat penting dalam dunia teknik mesin. Ketika sebuah batang lurus menerima beban momen puntir (torque) pada salah satu ujungnya, maka batang tersebut akan mengalami rotasi terhadap sumbu longitudinalnya. Fenomena inilah yang disebut sebagai deformasi torsional.
Pada batang berpenampang lingkaran, torsi menghasilkan sudut puntir (θ) di antara kedua ujung batang. Artinya, ketika salah satu ujung diputar, bagian ujung lainnya tetap atau bergerak dengan sudut tertentu sesuai besar gaya puntirnya. Menariknya, penampang melintang batang tidak mengalami perubahan bentuk, hanya terjadi rotasi kecil terhadap sumbu utamanya.
1. Prinsip Dasar Torsional
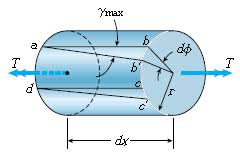
Untuk memahami deformasi ini, bayangkan sebuah batang logam silindris diputar di salah satu ujungnya. Elemen kecil di sepanjang batang akan mengalami pergeseran sudut yang sangat kecil, di mana titik-titik di permukaan luar mengalami regangan geser maksimum, sedangkan titik di sumbu pusat tidak mengalami regangan sama sekali.
Hubungan matematis antara momen puntir (T), tegangan geser (τ), dan sudut puntir (θ) diberikan oleh:
T/J=τ/r=
dengan:
-
T = momen torsi (N·m)
-
J = momen inersia polar penampang (m⁴)
-
τ = tegangan geser maksimum (Pa)
-
r = jari-jari batang (m)
-
G = modulus geser material (Pa)
-
L = panjang batang (m)
Rumus ini menggambarkan bahwa semakin besar torsi atau semakin kecil kekakuan material (G), maka sudut puntir akan semakin besar.
2. Torsi Tak Seragam
Dalam kenyataan, tidak semua batang menerima torsi konstan di sepanjang panjangnya. Kondisi ini disebut torsi tak seragam (non-uniform torsion). Kasus ini muncul ketika batang terdiri atas beberapa segmen dengan ukuran penampang berbeda, atau ketika beban puntir berubah secara kontinu di sepanjang batang.
Ada tiga kasus utama:
-
Batang dengan segmen-segmen prismatis yang mengalami torsi konstan di setiap segmen.
-
Batang dengan penampang berubah kontinu namun menerima torsi konstan.
-
Batang dengan penampang dan torsi yang bervariasi kontinu.
Analisis terhadap kondisi ini penting untuk menentukan titik-titik lemah, defleksi maksimum, dan desain poros transmisi agar tidak gagal akibat beban berulang.
3. Tabung Berdinding Tipis
Dalam aplikasi teknik, banyak komponen seperti poros pipa, tabung pesawat, dan poros kendaraan terbuat dari tabung berdinding tipis. Desain ini memberikan kekuatan torsional tinggi dengan berat yang lebih ringan.
Pada tabung berdinding tipis, tegangan geser (τ) lebih mudah dihitung dengan pendekatan sederhana:
τ=T/2Am.t
di mana:
-
Aₘ = luas area median dinding tabung
-
t = ketebalan dinding tabung
Desain seperti ini banyak diterapkan dalam poros penggerak (drive shaft) dan struktur pesawat terbang, di mana efisiensi berat menjadi faktor penting.
4. Aplikasi dalam Dunia Teknik Mesin
Pemahaman tentang deformasi torsional tidak hanya bersifat teoritis. Dalam praktiknya, konsep ini diterapkan dalam:
-
Analisis poros transmisi kendaraan agar tahan terhadap torsi tinggi.
-
Desain alat-alat putar seperti turbin dan generator.
-
Rekayasa material ringan dengan kekuatan puntir tinggi.
Melalui pembelajaran ini, mahasiswa diharapkan tidak hanya memahami rumus, tetapi juga mampu menghubungkan teori dengan fenomena nyata di dunia industri mekanik.